Comme son nom l’indique ce package permet de modéliser des graphes de Markov. Il est composé du module Markov. Son algorithme de calcul lui permet de gérer des graphes de plusieurs centaines d’états sans aucun problème.
Ce package permet de traiter des systèmes avec des dépendances temporelles (un événement devant se produire avant un autre) ou de gérer un nombre limité de réparateurs. Par sa nature, il représente tous les états possibles de l’élément étudié. Seul, il sera donc principalement utilisé pour des petits systèmes / équipements.
A noter qu’en plus des habituels temps passés dans les différents états et les probabilités d’être dans un état, le module Markov calcule également le taux de défaillance du système.

Markov
Multi-Phase
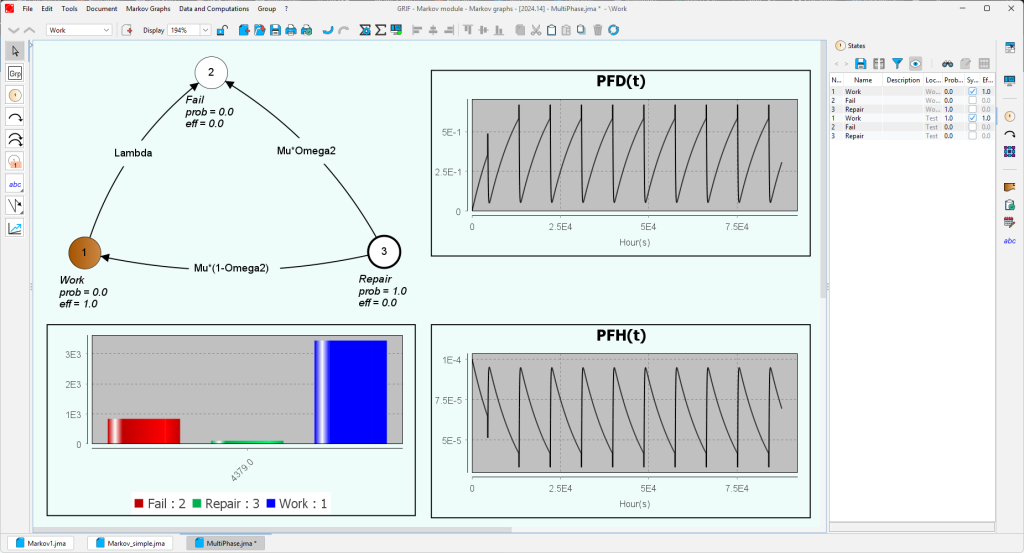
Les systèmes industriels ne se comportent pas forcément de la même manière tout au long de leur vie. Que ce soit pour des phases été/hiver, des phases stockage/fonctionnement ou maintenance/production, il est courant qu’un unique graphe de Markov ne puisse modéliser le système.
C’est pourquoi le module Markov permet de définir plusieurs graphes, chacun correspondant à une phase de la vie du système. Le module Markov peut ensuite effectuer un calcul de Markov multi-phases en enchaînant les différents graphes.
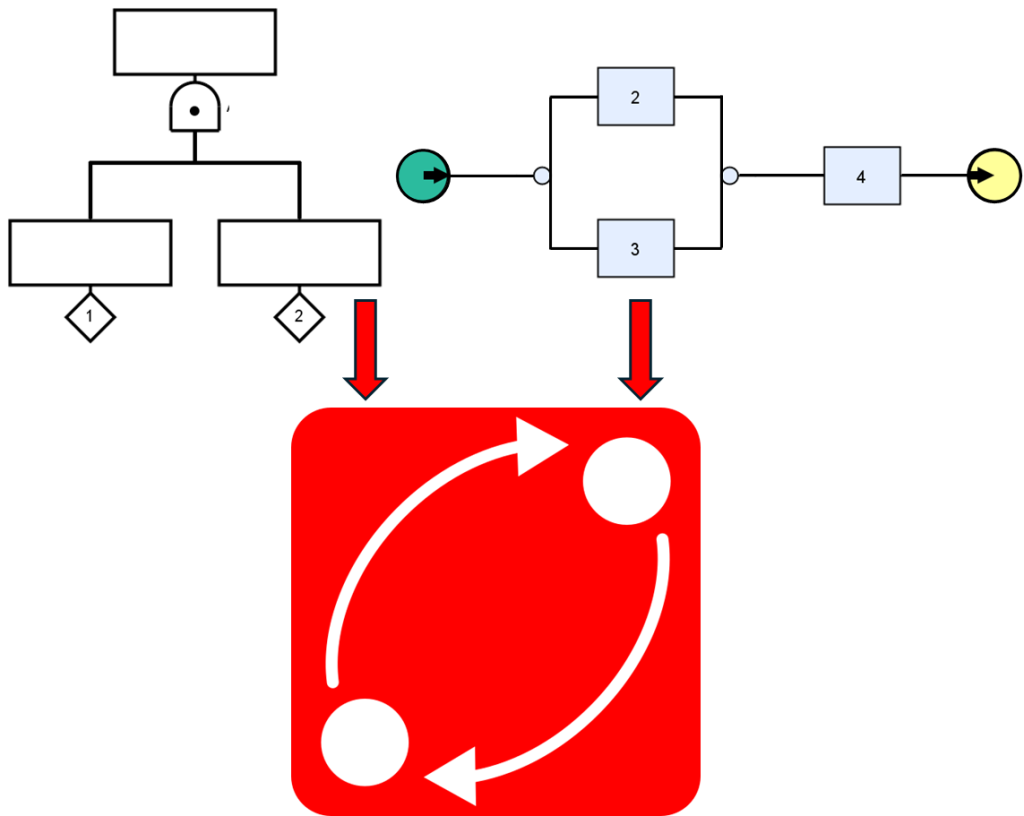
FT Driven Markov Graph
Couplé avec le package Booléen, le module Markov vous permettra de tirer pleinement partie des Fault-Tree driven Markov Graph, et des Reliability Block Diagram driven Markov Graph. Ces méthodes de modélisation permettent de créer des Graphes de Markov indépendants pour des équipements, puis de les assembler dans un modèle Booléen de plus haut niveau.
Si votre système est à 99% statique, à part le système d’alimentation en 1oo2 lui-même secondé par un groupe électrogène, l’envie de faire un arbre de défaillance est grande. Mais la partie alimentation ne peut être modélisée correctement par une approche Booléenne, c’est là que les FT driven Markov Graphs montrent leur intérêt.
